数据结构

背概念记算法。
GO！

绪论

全你妈是概念。
GO不住了，直接寄。
我的评价是直接跳：
heye神的数据结构笔记

1.2 基本概念及术语

  • 数据：对客观事物的符号表示，计算机科学中指所有能输入到计算机中并被计算机程序处理的符号的总称。

  • 数据元素：数据的基本单位。可以由若干个数据项组成。（类似结构体）

    注意：数据元素是数据的基本单位，数据项是数据的最小单位

  • 数据对象：性质相同的数据元素的集合。（比如说所有整型或者所有字符）

  • 数据结构：相互之间存在一种或多种特定关系的数据元素的集合。

数据元素之间的相互关系就是结构。
数据结构的形式表达为，其中数据元素上的有限集，是上关系的有限集。
一般有以下几种结构
- 集合：数据元素隶属于同一集合，除此之外没有其他关系
- 线性结构：数据元素存在一个对一个的关系
- 树形结构：数据元素存在一个对多个的关系
- 图状结构或网状结构：数据元素存在多个对多个的关系

>以上这几种结构还可以称为**逻辑结构**

  • 存储/物理结构：数据结构在计算机中的表示（又称映像）

    • 位：计算机中表示信息的最小单位，二进制中的一位。
    • 元素/结点：用一串位表示的数据元素（整型或者字符一类）
    • 数据域：数据元素由多个数据项组成，数据域就是对应各个数据项的子位串。

  • 顺序映像 顺序存储结构
    非顺序映像 链式存储结构

  • 数据类型：值的集合和定义在这个值集上的一组操作的总称。（例如整型变量，值集为整数，定义在其上的运算是加减乘除等计算）
    按照值的不同，数据类型分成两种：

    • 原子类型：不可再分。（比如说字符整型长整型浮点一类）
    • 结构类型：结构体或者数组。

  • 抽象数据类型（ADT）：是指一个数学模型以及定义在该模型上的一组操作。

    和数据类型差不多，但更强调数学层面，而且不再仅限于处理器自己定义的类型如整型一类，囊括了用户自己定义的数据类型

    分为三类：
    原子类型，固定聚合类型，可变聚合类型（后面两种可以统称为结构类型）

    D,S,P：数据对象，数据关系，基本操作。

  • 多形数据类型：是指其值的成分不确定的数据类型。（就是没写明变量是什么类型）

  • 存取结构
    顺序存储结构的存取结构是随机存取，链式存储结构的存取结构是顺序存取

1.4 算法

  • 五个重要特性：

    • 有穷性：在有穷步内结束，每一步都可以在有穷时间内完成。

    • 确定性：每一条指令都有确切的含义，不会有歧义。任何情况下算法都只有一条路径，对相同输入可以得到相同输出。

    • 可行性：可以用已有的基本运算执行有穷步来实现。

    • 输入：有零个或多个输入。

    • 输出：有一个或多个输出。

  • 算法设计的要求：

    • 正确性：程序对于精心选择的典型，苛刻而带有刁难性的几组输入数据能够得出满足规格说明的结果。（答案要对）

    • 可读性：要看得懂

    • 健壮性：输入非法可以察觉，不会被轻易弄崩。

    • 效率和低存储需求（高效性）：效率高，需求存储空间少。

  • 渐近时间复杂度（时间复杂度）：（基本操作的执行次数根据问题规模记作）

    • 频度 程序中某一语句被执行的次数。

给个练习：55.png

  • 空间复杂度：
    • 原地算法：空间复杂度为的算法。

第四章：串

KMP

假设串为T

  • 求next数组：
    1.首先让next[1]=0,next[2]=1
    2.从next[3]开始，假设为next[i]，则比较T[i-1]和T[next[i-1]]是否相等。
    3.如果相等，那么next[i]=next[i-1]+1
    4.如果不相等，就比较T[next[next[i-1]]]和T[i-1]是否相等，如果相等，那么next[i]=next[next[i-1]]+1
    5.如果还不相等，就比较T[next[next[next[i-1]]]]和T[i-1]是否相等，依次递推。
    6.依次递推。
    55.png
    55.png
  • 求nextval数组：
    只讲在next数组的基础上怎么求
    现在假设已经有了next[n]这个数组。
    1.首先让nextval[1]=0
    2.从nextval[2]开始，如果T[i]=T[next[i]],那么nextval[i]=nextval[next[i]],如果不相等,那么nextval[i]=next[i]
    3.依次递推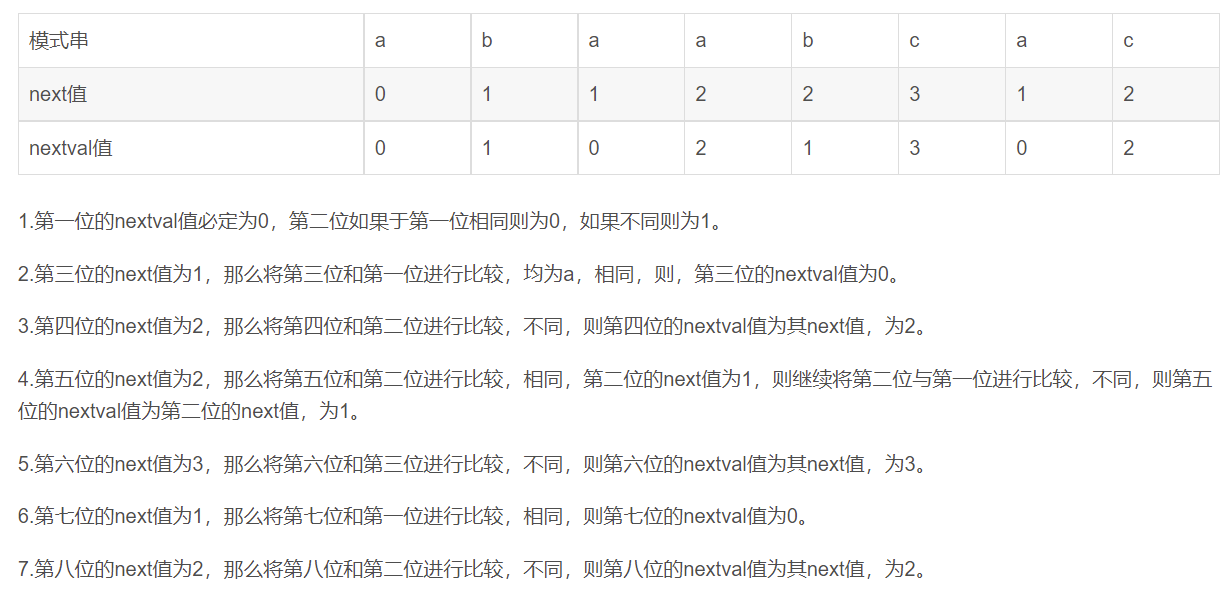
    55.png

第五章：数组和广义表

  • 寻址
    具体方法看例题。

55.png
66.png

矩阵的压缩存储

  • 对称矩阵
    66.png

下标公式推导：
只讨论的情况。
sa中的排列规则是从开始，对从小到大，列出所有，然后，重复这个过程，直到。
所以在列到第行的时候，sa一共有个元素。等差公式得到共有个元素，又因为sa中元素下标从0开始，所以第的下标为,的下标为。向后一个个加就可以得到的下标为。
和放在同一个位置，所以对调后照样算就是。

注意：因为对角线的存在，所以占用空间不是

  • 三角矩阵
    66.png

下三角矩阵的下标：
跟对称矩阵的排列规律是一样的，区别就是sa[0]=，所以在对称矩阵下标基础上+1，变成了。
上三角矩阵的下标：
与之前不同，上三角矩阵sa中的排列规则是从开始，对从小到大，列出所有，然后，重复这个过程，直到。即排列为：

所以列到第行的时候，sa一共有个元素，等差公式得到为个元素。因为下标从1开始，所以的下标为,往后递推得到的下标为。

  • 带状矩阵（对角矩阵）
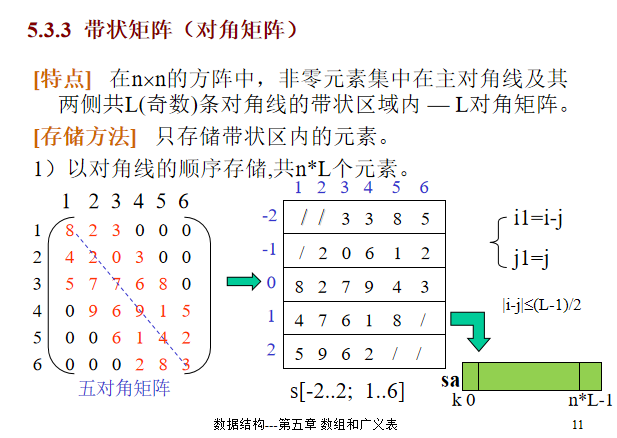
    66.png
    第一种，用矩阵存。
    图里写的很清楚，不赘述了。
    66.png
    第二种，用一维数组存。
    注意首行后和末行前都空了一个元素，这两行的元素是个。
    主对角线及其两侧共（奇数）条对角线的带状区域————对角矩阵。

随机稀疏矩阵

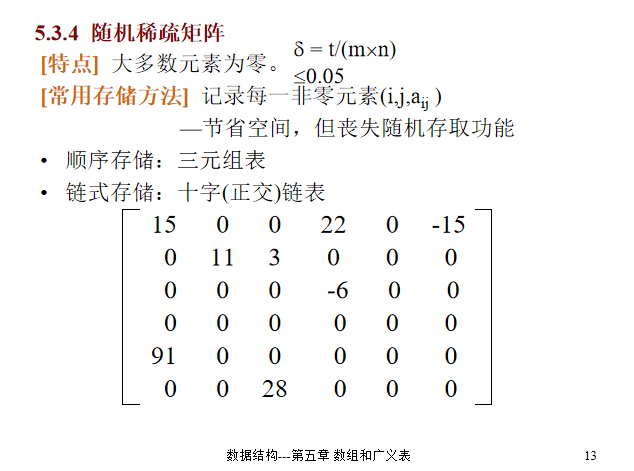
66.png
稀疏矩阵压缩之后，会失去随机存取的功能

- **三元组表**
![66.png](https://api2.mubu.com/v3/document_image/b752a570-43e0-4aaa-9cff-39763801def0-14970684.jpg)

- **三元组表的应用：矩阵转置**
![66.png](https://api2.mubu.com/v3/document_image/d2365e73-725d-4d3a-9045-49f565166a36-14970684.jpg)
有两种方法，普通转置和快速转置。
普通转置就是按列对原矩阵进行遍历。由于行数低的会优先出现，所以可以直接按元素在遍历时出现的顺序来行转列，列转行。
大致算法思路如下图：
![66.png](https://api2.mubu.com/v3/document_image/2ce62294-a984-4c5e-9957-e056f2990f81-14970684.jpg)
复杂度$O(n^2)$
**快速转置法**：
![66.png](https://api2.mubu.com/v3/document_image/db5d2ada-a489-407d-a816-9cb0290d3591-14970684.jpg)
大致实现思路：先遍历一遍原矩阵$a$得到num[]，然后通过num[]得到cpot[]（cpot[col]=cpot[col-1]+num[col-1]）。然后再遍历一次原矩阵，这次遍历把每个遍历到的元素直接放到$b$中对应的位置。（利用cpot，每次对应列有一个元素放入，就++cpot[col]，得到该列下一个元素在$b$中的位置）。
如图：
![66.png](https://api2.mubu.com/v3/document_image/108e822d-f350-47b5-b52b-adb693b519e9-14970684.jpg)
复杂度为$O(n)$。

下面这俩不是重点，看看就行。
- 行逻辑链接的表：
![66.png](https://api2.mubu.com/v3/document_image/78c62066-49f2-4d4e-9642-ce4be04bf26b-14970684.jpg)
Triple存的就是所有三元组。
rpos存的是每行第一个非零元素在矩阵中出现的位置。
- 十字（正交）链表
![66.png](https://api2.mubu.com/v3/document_image/645e4b52-63eb-4a72-949d-b558779d4409-14970684.jpg)
![66.png](https://api2.mubu.com/v3/document_image/a1bef51f-b9f3-4071-86fa-6bb3ead38d95-14970684.jpg)
在十字链表中插结点，要在行表中插一次，列表中插一次。

广义表

原子：逻辑上不能再分解的元素
子表：作为广义表中元素的广义表
66.png
注意：表尾不是指最后一个元素，而是除了第一个元素之外的所有元素。

  • 图形表达方式：圆圈是表，矩形是原子
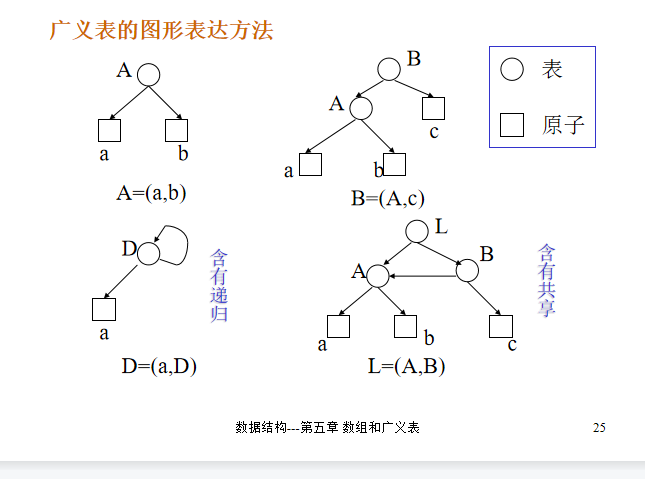
  • 66.png
  • 广义表分类
    • 纯表：和树型结构对应的广义表
    • 再入表：允许结点共享的广义表
    • 递归表：允许递归的广义表
      线性表纯表再入表递归表
  • 广义表的存储结构
    两种存储结构：
    • 头尾链表存储
      1
      2
      3
      4
      5
      6
      7
      8
      9
      10
      11
      typedef enum {ATOM, LIST} ElemTag;
      // ATOM==0:原子；LIST==1：子表
      typedef struct GLNode{
      	ElemTag  tag;
      	union {
      	     AtomType  atom;
      	     struct  {
      	          struct GLNode  *hp, *tp;
      	     }ptr;
      	}
      } * GList1;
      在结构体定义里用联合区别了原子和子表，tag用来表明类型。tag=0为原子结点，tag=1为表结点。
      示例图：
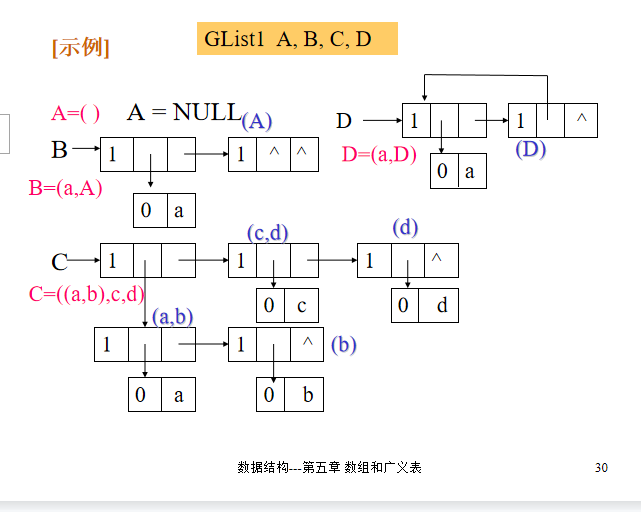
      66.png
    注意：由于原子结点没有后继指针，所以每个原子结点都要搭配一个表结点，这个表结点的hp指向原子结点，tp指向后继。
    • 扩展的线性链表形式
      1
      2
      3
      4
      5
      6
      7
      8
      9
      10
      11
      12
      typedef enum {ATOM, LIST} ElemTag;
      // ATOM==0:原子；LIST==1：子表
      typedef struct GLNode{
      	ElemTag  tag;
      	union {
      	     AtomType  atom;
      	     struct  {
                 struct GLNode  *hp;
            }
       }
       struct GLNode  *tp;
      } * GList2;
    与上一种的区别在于这里的原子结点也有后继指针。这一点更符合直觉。
    示例图：
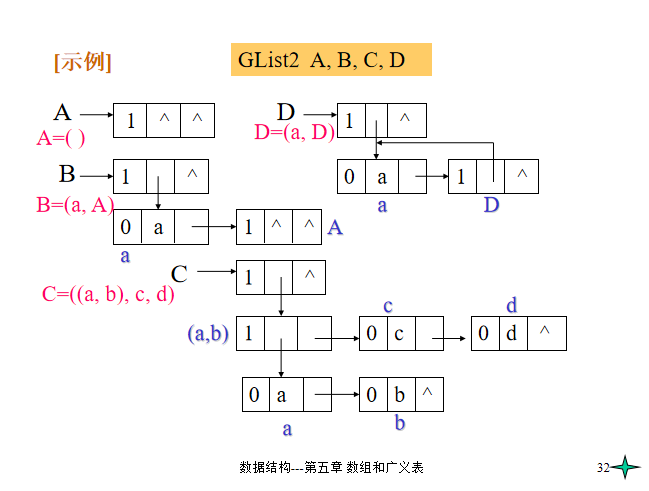
    66.png
    • *广义表的递归算法
      • 计算广义表的深度
        • 方法一：
          基本项：
          DEPTH(LS)=1;（LS为空表）
          DEPTH(LS)=0;（LS为原子）
          归纳项：
          DEPTH(LS)=1+max{DEPTH()}
          1
          2
          3
          4
          5
          6
          7
          8
          9
          10
          int GListDepth(GList1 L)
          {       
              if  (!L) return 1;   //空表
              if  (L->tag==ATOM) return 0;  //单原子
              for (max=0, pp=L; pp; pp=pp->ptr.tp) {
                    dep=GListDepth (pp->ptr.hp);
                    if (dep>max) max=dep;
             }
             return  max+1;
          }//GListDepth
          遍历的是tp，递归访问的是hp。
          同时因为hp比上一结点的层次低1，所以return是max+1.
        注意：max是一个全局变量
        • 方法二：
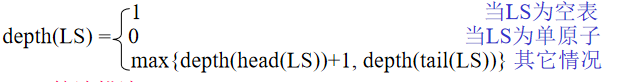          66.png
          1
          2
          3
          4
          5
          6
          7
          8
          9
           int GListDepth(GList1 L)
          {        
              if  (!L) return 1;   //空表
              if  (L->tag==ATOM) return 0;  //单原子
              dep1=GListDepth (L->ptr.hp)+1;
              dep2=GListDepth (L->ptr.tp);
              if  (dep1>dep2)  return dep1;
              else   return  dep2;
          }//GListDepth
          hp+1是因为头结点比原结点低一层，而尾结点和原结点同层。
      • 复制广义表
        如果空了就复制NULL；
        如果是原子就复制单原子；
        如果是表就分别复制头和尾；
        1
        2
        3
        4
        5
        6
        7
        8
        9
        10
        11
        12
        13
        14
        Status CopyGList(GList1 &T, GList1 L)
        {        if  (!L) T=NULL;   //复制空表
         else {
            T=(GList1)malloc(sizeof(GLNode));
            if (!T) exit(OVERFLOW);
            T->tag=L->tag;
            if (L->tag==ATOM) T->atom=L->atom; //复制单原子
            else {
                 CopyGList(T->ptr.hp, L->ptr.hp);
                 CopyGList(T->ptr.tp, L->ptr.tp);
            }
         }
         return  OK;
         }//CopyGList

第九章：二叉树

  • 有n个结点的二叉树的形态数目
    套公式，有种。

  • 术语：

    • 结点的度：结点拥有的子树数目
    • 叶子（终端）结点：度为0的结点
    • 分支（非终端）结点：度不为0的结点
    • 树的度：树的各结点度的最大值
    • 内部结点：除根结点之外的分支结点
    • 双亲与孩子（结点）：结点的子树的根称为该结点的孩子，该结点称为孩子的双亲
    • 兄弟：属于同一双亲的孩子
    • 结点的祖先：从根到该结点所经分支上的所有结点
    • 结点的子孙：该结点为根的子树中的任一结点
    • 结点的层次：表示该结点在树上的相对位置。根在第一层，其他的结点依次下推，若某结点在第层上，则其孩子在第层上。
    • 堂兄弟；